Kiį»m tra tĆnh nguyĆŖn tį» xĆ”c suįŗ„t
Äį» thiįŗæt lįŗp hį» mįŗt RSA, ta phįŗ£i tįŗ”o ra cĆ”c sį» nguyĆŖn tį»
ngįŗ«u nhiĆŖn lį»n (chįŗ³ng hįŗ”n cĆ³ 80 chį»Æ sį»). Trong thį»±c tįŗæ, phĘ°Ę”ng cĆ”ch thį»±c hiį»n
Äiį»u nĆ y lĆ : trĘ°į»c hįŗæt phįŗ£i tįŗ”o ra cĆ”c sį» ngįŗ©u nhiĆŖn lį»n, sau ÄĆ³ kiį»m tra tĆnh
nguyĆŖn thuį»· cį»§a chĆŗng bįŗ±ng cĆ”ch dĆ¹ng thuįŗt toĆ”n xĆ”c suįŗ„t Monte- Carlo thį»i gian
Äa thį»©c (chįŗ³ng hįŗ”n nhĘ° thuįŗt toĆ”n Miller- Rabin hoįŗ·c lĆ thuįŗt toĆ”n Solovay-
Strasen). Cįŗ£ hai thuįŗt toĆ”n trĆŖn Äį»u ÄĘ°į»£c trƬnh bĆ y trong phįŗ§n nĆ y. ChĆŗng lĆ
cĆ”c thuįŗt toĆ”n nhanh (tį»©c lĆ mį»t sį» nguyĆŖn n ÄĘ°į»£c kiį»m tra trong thį»i Äa thį»©c
theo log2n, lĆ sį» cĆ”c bĆt trong biį»u diį»n nhį» phĆ¢n cį»§a n). Tuy
nhiĆŖn, vįŗ«n cĆ³ khįŗ£ nÄng lĆ thuįŗn toĆ”n cho rįŗ±ng n lĆ sį» nguyĆŖn tį» trong khi thį»±c
tįŗæ n lĆ hį»£p lį» sį». Bį»i vįŗy, bįŗ±ng cĆ”ch thay Äį»i thuįŗt toĆ”n nhiį»u lįŗ§n, cĆ³ thį»
giįŗ£m xĆ”c suįŗ„t sai sį» dĘ°į»i mį»t mį»©c ngĘ°į»”ng cho phĆ©p (sau nĆ y sįŗ½ thįŗ£o luįŗn kį»¹ hĘ”n
mį»t chĆŗt vį» vįŗ„n Äį» nĆ y).
Mį»t vįŗ„n Äį» quan trį»ng khĆ”c:
lĆ cįŗ§n phįŗ£i kiį»m tra bao nhiĆŖu sį» nguyĆŖn ngįŗ«u nhiĆŖn (vį»i kĆch thĘ°Ę”c xĆ”c
Äį»nh)cho tį»i khi tƬm ÄĘ°į»£c mį»t sį» nguyĆŖn tį». Mį»t kįŗæt quįŗ£ nį»i tiįŗæng trong lĆ½
thuyįŗæt sį» (ÄĘ°į»£c gį»i lĆ Äį»nh lĆ½ sį» nguyĆŖn tį») phĆ”t biį»u rįŗ±ng: sį» cĆ”c sį» nguyĆŖn
tį» khĆ“ng lį»n hĘ”n N xįŗ„p xį» bįŗ±ng N/ln N. Bį»i vįŗy, nįŗæu p ÄĘ°į»£c chį»n ngįŗ«u nhiĆŖn thƬ
xĆ”c suįŗ„t p lĆ mį»t sį» nguyĆŖn tį» sįŗ½ vĆ o khoįŗ£ng 1/ln p. Vį»i mį»t moÄun 512 bĆt, ta
cĆ³ 1/ln p įŗ± 1/77. Äiį»u nĆ y cĆ³
nghÄ©a lĆ tĆnh trung bƬnh, cĘ° 177 sį» nguyĆŖn ngįŗ«u nhiĆŖn p vį»i kĆch thĘ°į»c tĘ°Ę”ng
į»©ng sįŗ½ cĆ³ mį»t sį» lĆ sį» nguyĆŖn tį». DÄ© nhiĆŖn, nįŗæu chÄ© hįŗ”n chįŗæ xĆ©t cĆ”c sį» nguyĆŖn
lįŗ» thƬ xĆ”c suįŗ„t sįŗ½ tÄng gįŗ„p ÄĆ“i tį»i khoįŗ£ng 2/177). Bį»”i vįŗy trĆŖn thį»±c tįŗæ, hoĆ n
toĆ n cĆ³ khįŗ£ nÄng tįŗ”o ÄĘ°į»£c cĆ”c nguyĆŖn tį» Äį»§ lį»n vĆ do ÄĆ³ vį» mįŗ·t thį»±c thį» ta cĆ³
thį» thiįŗæt lįŗp ÄĘ°į»£c mį»t hį» mįŗt RSA. Sau ÄĆ¢y sįŗ½ tiįŗæp tį»„c xem xĆ©t Äiį»u nĆ y ÄĘ°į»£c
thį»±c hiĆŖn nhĘ° thįŗæ nĆ o.
Mį»t bĆ i toĆ”n quyįŗæt Äį»nh lĆ mį»t bĆ i toĆ”n toĆ”n trong ÄĆ³
mį»t cĆ¢u hį»i cįŗ§n ÄĘ°į»£c trįŗ£ lį»i cĆ³ hoįŗ·c khĆ“ng. Mį»t thuįŗt toĆ”n xĆ”c suįŗ„t lĆ mį»t
thuįŗt toĆ”n bįŗ„t kį»³ cĆ³ sį» dį»„ng cĆ”c sį» ngįŗ«u nhiĆŖn (ngĘ°į»£c lįŗ”i, thuįŗt toĆ”n khĆ“ng sį»
dį»„ng cĆ”c sį» ngįŗ«u nhiĆŖn sįŗ½ ÄĘ°į»£c gį»i lĆ mį»t thuįŗt toĆ”n tįŗ„t Äį»nh). CĆ”c Äį»nh nghÄ©a
sau cĆ³ liĆŖn quan tį»i cĆ”c thuįŗt toĆ”n xĆ”c suįŗ„t cho cĆ”c bĆ i toĆ”n quyįŗæt Äį»nh.
Äį»nh nghÄ©a 4.1
Thuįŗt toĆ”n Monte Carlo Äį»nh
hĘ°į»ng cĆ³ lĆ mį»t thuįŗt toĆ”n xĆ”c suįŗ„t cho mį»t bĆ i toĆ”n quyįŗæt Äį»nh, trong ÄĆ³ cĆ¢u
trįŗ£ lį»i cĆ³ luĆ“n luĆ“n lĆ ÄĆŗng cĆ²n cĆ¢u trįŗ£ lį»i khĆ“ng cĆ³ thį» lĆ sai. Thuįŗt toĆ”n
Monte Carlo Äį»nh hĘ°į»ng khĆ“ng cÅ©ng ÄĘ°į»£c Äį»nh nghÄ©a theo cĆ”ch tĘ°Ę”ng tį»±. ChĆŗng
ta nĆ³i rįŗ±ng, mį»t thuįŗt toĆ”n Monte Carlo Äį»nh hĘ°į»ng cĆ³ cĆ³ xĆ”c suįŗ„t sai bįŗ±ng e nįŗæu vį»i bįŗ„t kį»³ mį»t trĘ°į»ng
hį»£p nĆ o mĆ cĆ¢u trįŗ£ lį»i lĆ cĆ³ thƬ thuįŗt toĆ”n cĆ³ cĆ¢u trįŗ£ lį»i sai khĆ“ng vį»i
xĆ”c suįŗ„t khĆ“ng lį»n hĘ”n e (xĆ”c
suįŗ„t nĆ y ÄĘ°į»£c tĆnh trĆŖn mį»i phĆ©p chon ngįŗ«u nhiĆŖn, cĆ³ thį» thį»±c hiĆŖn bį»i thuįŗt
toĆ”n vį»i mį»t cĆ¢u vĆ o ÄĆ£ cho).
BĆ i toĆ”n quyįŗæt Äį»nh į» ÄĆ¢y lĆ
bĆ i toĆ”n hį»£p lį» sį» mĆ“ tįŗ£ į» hƬnh 4.5.
Cįŗ§n chĆŗ Ć½ rįŗ±ng mį»t thuįŗt toĆ”n quyįŗæt Äį»nh chį» cĆ³ cĆ¢u trįŗ£
lį»i cĆ³ hoįŗ·c khĆ“ng Äįŗ·c biį»t trong bĆ i toĆ”n hį»£p lį» sį» lĆ ta khĆ“ng yĆŖu cįŗ§u
thuįŗt toĆ”n tĆnh tĆch thį»«a sį» khi n lĆ hį»£p lį» sį».
TrĘ°į»c tiĆŖn ta sįŗ½ mĆ“ tįŗ£ thuįŗt
toĆ”n Soloway- Strasson. ÄĆ¢y lĆ mį»t thuįŗt toĆ”n Monte- Carlo Äį»nh hĘ°į»ng cĆ³ cho
bĆ i toĆ”n hį»£p sį» cĆ³
TrĘ°į»c tiĆŖn ta sįŗ½ mĆ“ tįŗ£
thuįŗt toĆ”n Soloway- Strasson. ÄĆ¢y lĆ mį»t thuįŗt toĆ”n Monte-Carlo Äį»nh
hĘ°į»ng cĆ³ cho bĆ i toĆ”n hį»£p sį» vĆ xĆ”c xuįŗ„t sai 1/2. Bį»i vįŗy, nįŗæu thuįŗt toĆ”n trįŗ£
lį»i cĆ³ thƬ n lĆ hį»£p sį»; ngĘ°į»£c lįŗ”i nįŗæu n lĆ hį»£p sį» thƬ thuįŗt toĆ”n trįŗ£ lį»i cĆ³
vį»i xĆ”c xuįŗ„t tį»i thiį»u 1/2.
HƬnh 4.5. BĆ i toĆ”n hį»£p sį».
Äįŗ·c trĘ°ng cį»§a bĆ i toĆ”n: mį»t sį» nguyĆŖn dĘ°Ę”ng n ³ 2 CĆ¢u hį»i: n
cĆ³ phįŗ£i lĆ hį»£p sį» khĆ“ng ?
HƬnh 4.6. BĆ i toĆ”n vį» cĆ”c thįŗ·ng dĘ° bįŗc hai.
Äįŗ·c trĘ°ng cį»§a bĆ i toĆ”n:
cho p lĆ mį»t sį» nguyĆŖn tį» lįŗ» vĆ mį»t sį» nguyĆŖn x sao cho 0 Ć x Ć
p-1 CĆ¢u hį»i: x cĆ³ phįŗ£i lĆ thįŗ·ng dĘ° bįŗc hai phĆ©p modulo
p ?
Mįŗ·c dĆ¹ thuįŗt toĆ”n
Miller-Rabin (ta sįŗ½ xĆ©t sau) nhanh hĘ”n thuįŗt toĆ”n Soloway-Strasson (S-S) nhĘ°ng
ta sįŗ½ xĆ©t thuįŗt toĆ”n S-S trĘ°į»c vƬ nĆ³ dį»
hiį»u hĘ”n vį» khĆ”i niį»m, Äį»ng thį»i lįŗ”i
liĆŖn quan tį»i mį»t sį» vįŗ„n Äį» cį»§a lĆ½ thuyįŗæt sį» (mĆ ta sįŗ½ cĆ²n dĆ¹ng trong cĆ”c
chĘ°Ę”ng trƬnh sau). Ta sįŗ½ xĆ¢y dį»±ng mį»t sį» nį»n tįŗ£ng sĆ¢u sįŗÆc hĘ”n trong lĆ½ thuyįŗæt
sį» trĘ°į»c khi mĆ“ tįŗ£ thuįŗt toĆ”n.
Äį»nh nghÄ©a 4.2.
Giįŗ£ sį» p lĆ mį»t sį» nguyĆŖn tį»
lįŗ» vĆ x lĆ mį»t sį» nguyĆŖn, 1 Ć x Ć p-1. x ÄĘ°į»£c gį»i lĆ thįŗ·ng dĘ°
bįŗc hai theo modulo p nįŗæu phĘ°Ę”ng trƬnh Äį»ng dĘ° y2 ŗ x (modulo p) cĆ³ mį»t nghiį»m yĘ°įŗ»Zp x ÄĘ°į»£c gį»i lĆ
thįŗ·ng dĘ° khĆ“ng bįŗc hai theo modulo p nįŗæu x ??? 0 (mod p) vĆ x khĆ“ng phįŗ£i lĆ
thįŗ·ng dĘ° bįŗc hai theo modulo p.
VĆ dį»„ 4.6.
CĆ”c thįŗ·ng dĘ° bįŗc hai theo modulo 11 lĆ 1,3,4,5 vĆ 9.
Cįŗ§n Äį» Ć½ rįŗ±ng, (±1)2=1, (±5)2=3, (±2)2=4, (±4)2=5, (±3)2=9 (į» ÄĆ¢y tįŗ„t
cįŗ£ cĆ”c phĆ©p sį» hį»c Äį»u thį»±c hiį»n trong Z11).
BĆ i toĆ”n quyįŗæt Äį»nh thįŗ·ng dĘ°
bįŗc hai ÄĘ°į»£c trƬnh bĆ y trĆŖn hƬnh 4.6 sįŗ½ ÄĘ°į»£c thįŗ„y mį»t cĆ”ch tĘ°Ę”nngf minh nhĘ°
sau:
TrĘ°į»c hįŗæt, ta sįŗ½ chį»©ng minh
mį»t kįŗæt quįŗ£- tiĆŖu chuįŗ©n Euler tįŗ”o
nĆŖn thuįŗt toĆ”n tįŗ„t Äį»nh theo thį»i gian Äa thį»©c cho bĆ i toĆ”n vį» cĆ”c thįŗ·ng dĘ° bįŗc
hai.
Äį»nh lĆ½ 4.8. (TiĆŖu chuįŗ©n Euler)
Giįŗ£ sį» p lĆ mį»t sį» nguyĆŖn tį», khi ÄĆ³ x lĆ mį»t
thįŗ·ng dĘ° bįŗc hai theo modulo p khi vĆ chį» khi:
x(p-1)/2
ŗ1 (mod p)
Chį»©ng minh:
![]() TrĘ°į»c
hįŗæt giįŗ£ sį» rįŗ±ng, xŗy2(mod p).
Theo hį» quįŗ£ 4.6, nįŗæu p lĆ sį» nguyĆŖn tį» thƬ xp-1ŗ1 (mod p) vį»i mį»i x ŗ 0 (mod p). Bį»i vįŗy ta cĆ³ :
TrĘ°į»c
hįŗæt giįŗ£ sį» rįŗ±ng, xŗy2(mod p).
Theo hį» quįŗ£ 4.6, nįŗæu p lĆ sį» nguyĆŖn tį» thƬ xp-1ŗ1 (mod p) vį»i mį»i x ŗ 0 (mod p). Bį»i vįŗy ta cĆ³ :
x(p-1)/2
ŗ (y2)(p-1)/2
(mod p)
ŗyp-1(mod p)
ŗ1 (mod p)
NgĘ°į»£c lįŗ”i, giįŗ£ sį» rįŗ±ng x(p-1)/2ŗ1 (mod p). Cho p lĆ mį»t phįŗ§n
tį» nguyĆŖn thuį»· theo modulo p. Khi ÄĆ³ xŗbi
(mod p) vį»i giĆ” trį» i nĆ o ÄĆ³. Ta cĆ³
x(p-1)/2 ŗ (bi)(p-1)/2
(mod p)
ŗbi(p-1)/2(mod p)
VƬ p cĆ³ bįŗc bįŗ±ng
p-1 nĆŖn p-1 phįŗ£i lĆ Ę°į»c cį»§a i(p-1)/2. Bį»i vįŗy i lĆ sį» chįŗµn vĆ nhĘ° vįŗy cÄn bįŗc
hai cį»§a x lĆ ±bi/2.;
Äį»nh lĆ½ 4.8 sįŗ½ dįŗ«n tį»i mį»t
thuįŗt toĆ”n thį»i gian Äa thį»©c cho cĆ”c thįŗ·ng dĘ° bįŗc hai nhį» sį» dį»„ng kį»¹ thuįŗt
bƬnh phĘ°Ę”ng vĆ nhĆ¢n cho phĆ©p lįŗ„y luį»¹ thį»«a theo modulo p. Äį» phį»©c tįŗ”p cį»§a
thuįŗt toĆ”n khoįŗ£ng O((log p)3).
Sau ÄĆ¢y tiįŗæp tį»„c ÄĘ°a ra mį»t sį» Äį»nh nghÄ©a tį»« lĆ½ thuyįŗæt
sį»:
Äį»nh nghÄ©a 4.3.
Giįŗ£ sį» p lĆ sį» nguyĆŖn tį» lįŗ». Vį»i mį»t sį» nguyĆŖn tį» bįŗ„t
kį»³ a ³0, ta
![]()
Äį»nh nghÄ©a kĆ½ hiį»u
Legendre nhĘ° sau:
![]()
![]()
0
nįŗæu a ŗ 0 (mod p)
= 1 nįŗæu
lĆ thÄng dĘ° bįŗc hai theo modulo p
![]() -1 nįŗæu lĆ thÄng dĘ°
khĆ“ng bįŗc hai theo modulo p
-1 nįŗæu lĆ thÄng dĘ°
khĆ“ng bįŗc hai theo modulo p
Ta ÄĆ£ biįŗæt lĆ a(p-1)/2ŗ 1 (mod p) khi vĆ chį» khi a
lĆ mį»t thįŗ·ng dĘ° bįŗc hai theo modulo p. Nįŗæu a lĆ bį»i cį»§a p thƬ rƵ rĆ ng a(p-1)/2ŗ 0(mod p). Cuį»i cĆ¹ng, nįŗæu a
lĆ mį»t thįŗ·ng dĘ° khĆ“ng bįŗc hai theo modulo p thƬ a(p-1)ŗ -1 (mod p) vƬ ap-1ŗ1(mod p). Bį»i vįŗy, ta cĆ³ kįŗæt
quįŗ£ cho phĆ©p xĆ¢y dį»±ng mį»t thuįŗt toĆ”n hį»Æu hiį»u Äį» ÄĆ”nh giĆ” cĆ”c kĆ½ hiį»u Legendre
nhĘ° sau
Äį»nh LĆ½ 4.9.
![]()
Giįŗ£ sį» p lĆ mį»t sį» nguyĆŖn tį». Khi ÄĆ³ ŗ a(p-1)/2
(mod p).
![]()
Sau ÄĆ¢y lĆ mį»t Äį»nh nghÄ©a
tį»ng quĆ”t hoĆ” cho kĆ½ hiį»u Legendre.
Äį»nh nghÄ©a 4.4.
Giįŗ£ sį» n lĆ mį»t sį» nguyĆŖn
dĘ°Ę”ng lįŗ» vĆ phĆ¢n tĆch theo cĆ”c luį»¹ thį»«a nguyĆŖn tį» cį»§a n lĆ p1e1
....... pKek . Giįŗ£ sį» a ³ 0 lĆ
mį»t sį» nguyĆŖn. KĆ½ hiį»u
Jacobi
ÄĘ°į»£c Äį»nh nghÄ©a nhĘ° sau:
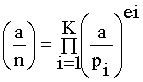
![]()
VĆ dį»„ 4.7.
![]()
XĆ©t kĆ½ hiį»u Jacobi . PhĆ¢n tĆch luį»¹ thį»«a nguyĆŖn tį» cį»§a
9975 lĆ : 9975=3 x 52 x 7 x
19. Bį»i vįŗy ta cĆ³:
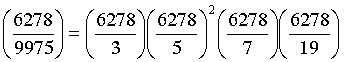
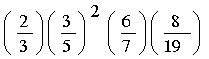
=
=(-1)(-1)2(-1)(-1)
= -1.
Giįŗ£ sį» n > 1 lĆ mį»t sį» lįŗ».
Nįŗæu n lĆ mį»t sį» nguyĆŖn tį» thƬ ŗ
a(n-1)/2 (mod n) vį»i a bįŗ„t kį»³. Mįŗ·t khĆ”c nįŗæu
n lĆ mį»t hį»£p sį» thƬ Äį»ng dĘ° thį»©c trĆŖn cĆ³ thį» ÄĆŗng hoįŗ·c khĆ“ng. Nįŗæu phĘ°Ę”ng trƬnh
ÄĆ³ vįŗ«n ÄĆŗng thƬ a ÄĘ°į»£c gį»i
lĆ sį» giįŗ£ nguyĆŖn tį» Euler theo cĘ” sį» n. VĆ dį»„: 10 lĆ sį»
giįŗ£ nguyĆŖn tį» Euler
![]()
theo cĘ” sį» 91 vƬ :
![]()
= -1 = 1045 mod 91
![]()
Tuy nhiĆŖn cĆ³ thį» chį»©ng tį»
rįŗ±ng, vį»i mį»t hį»£p sį» lįŗ» n bįŗ„t kį»³, sįŗ½ cĆ³p nhiį»u nhįŗ„t mį»t nį»a cĆ”c sį» nguyĆŖn a
(sao cho 1 Ć a Ć n-1) lĆ cĆ”c sį» giįŗ£ nguyĆŖn tį»
Euler cĘ” sį» n (xem cĆ”c bĆ i tįŗp). Äiį»u ÄĆ³ chį»©ng tį» rįŗ±ng, viį»c kiį»m tra tĆnh
nguyĆŖn tį» theo thuįŗt toĆ”n Soloway-Strasson ÄĘ°į»£c nĆŖu į» hƬnh 4.7 lĆ thuįŗt toĆ”n
Monte-Carlo Äį»nh hĘ°į»ng cĆ³vį»i xĆ”c xuįŗ„t sai tį»i Äa lĆ 1/2.
Äįŗæn ÄĆ¢y vįŗ«n chĘ°a xĆ”c Äį»nh rƵ thuįŗt toĆ”n ttrĆŖn cĆ³ theo
thį»i gian Äa thį»©c hay khĆ“ng.
Ta ÄĆ£ biįŗæt cĆ”ch ÄĆ”nh giĆ” a(n-1)/2
(mod n) trong thį»i gian Äa thį»©c
O((log n)3), tuy nhiĆŖn cįŗ§n phįŗ£i lĆ m thįŗæ nĆ o
Äį» tĆnh cĆ”c kĆ½ hiį»u Jacobi mį»t cĆ”ch cĆ³ hiį»u quįŗ£. VƬ kĆ½ hiį»u Jacobi ÄĘ°į»£c xĆ”c
Äį»nh theo cĆ”c thį»«a sį» trong phĆ¢n tĆch cį»§a n. Tuy nhiĆŖn nįŗæu cĆ³ thį» phĆ¢n tĆch
ÄĘ°į»£c n thƬ ta ÄĆ£ biįŗæt nĆ³ cĆ³ phįŗ£i lĆ sį» nguyĆŖn tį» hay khĆ“ng, bį»i vįŗy cĆ”ch lĆ m
nĆ y sįŗ½ dįŗ«n tį»i mį»t vĆ²ng luįŗ©n quįŗ©n.
HƬnh 4.7. Thuįŗt toĆ”n kiį»m tra tĆnh nguyĆŖn tį»
Solova-Strassen vį»i sį»
nguyĆŖn lįŗ» n.
|
1. Chį»n mį»t
sį» nguyĆŖn ngįŗ«u nhiĆŖn a, 1 Ć a Ć n-1 2. Nįŗæu ŗ a(n-1)/2
(mod n) thƬ
Trįŗ£ lį»i n lĆ sį» nguyĆŖn tį» Nįŗæu khĆ“ng
Trįŗ£ lį»i n lĆ mį»t hį»£p sį» |
Rįŗ„t may lĆ cĆ³ thį» ÄĆ”nh giĆ” kĆ½
hiį»u Jacobi mĆ khĆ“ng cįŗ§n phįŗ£i phĆ¢n tĆch n nhį» sį» dį»„ng mį»t sį» kįŗæt quįŗ£ cį»§a lĆ½
thuyįŗæt sį», trong ÄĆ³ kįŗæt quįŗ£ quan trį»ng nhįŗ„t lĆ tĆnh chįŗ„t 4 (tį»ng quĆ”t hoĆ” luįŗt
tĘ°Ę”ng hį» bįŗc hai ).
Ta sįŗ½ liį»t kĆŖ mĆ khĆ“ng chį»©ng minh cĆ”c tĆnh chįŗ„t nĆ y.
![]()
1. Nįŗæu n
lĆ mį»t sį» nguyĆŖn tį» lįŗ» vĆ m1 ŗ m2
(mod n) thƬ:
![]()
![]()
=
2. Nįŗæu n lĆ mį»t sį» nguyĆŖn lįŗ»
thƬ
![]() 1
nįŗæu n ŗ ± 1 (mod 8)
1
nįŗæu n ŗ ± 1 (mod 8)
=
-1 nįŗæu n ŗ ± 3 (mod 8)
3. Nįŗæu n lĆ mį»t sį» nguyĆŖn lįŗ» thƬ
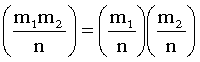
![]()
Äįŗ·c biį»t nįŗæu m=2kt
vį»i t lĆ mį»t sį» lįŗ» thƬ:
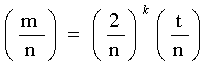
4. Giįŗ£ sį» m
vĆ n lĆ cĆ”c sį» nguyĆŖn lįŗ», khi ÄĆ³:
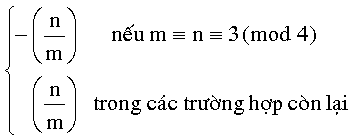
=
vĆ dį»„
Äį» minh hoįŗ” cho viį»c Ć”p dį»„ng cĆ”c tĆnh chįŗ„t trĆŖn , ta sįŗ½
ÄĆ”nh giĆ” kĆ
![]()
![]()
hiį»u Jacobi nhĘ° trong bįŗ£ng dĘ°į»i ÄĆ¢y. Cįŗ§n chĆŗ Ć½ lĆ trong vĆ dį»„
nĆ y, ta ÄĆ£ sį» dį»„ng liĆŖn tiįŗæp cĆ”c tĆnh chįŗ„t4, 1,3 ,vĆ 2.
NĆ³i chung, bįŗ±ng cĆ”ch Ć”p dį»„ng
4 tĆnh chįŗ„t trĆŖn, cĆ³ thį» tĆnh toĆ”nkĆ
![]()
hiį»u Jacobi trong thį»i gian Äa thį»©c. CĆ”c phĆ©p tĆnh
sį» hį»c dĆ¹ng į» ÄĆ¢y
chį» lĆ rĆŗt gį»n theo modulo vĆ phĆ¢n tĆch ra cĆ”c luį»¹ thį»«a
cį»§a thuįŗt toĆ”n ÄĘ°į»£c biį»u diį»
n dĘ°į»i dįŗ”ng nhį» phĆ¢n thƬ viį»c phĆ¢n tĆch ra cĆ”c luį»¹
thį»«a cį»§a hai sį» chĆnh lĆ viį»c xĆ”c Äį»nh sį» cĆ”c sį» 0 tiįŗæp sau. Bį»i vįŗy, Äį» phį»©c
tįŗ”p cį»§a thuįŗt toĆ”n ÄĘ°į»£c xĆ”c Äį»nh bį»i sį» cĆ”c phĆ©p rĆŗt gį»n theo modulo cįŗ§n tiįŗæn
hĆ nh. KhĆ“ng khĆ³ khÄn lįŗÆm cĆ³ thį» chį»©ng tį» rįŗ±ng, cįŗ§n thį»±c hiį»n nhiį»u nhįŗ„t lĆ .
=
. =
= = = = = = = = -1 theo tĆnh chįŗ„t
2
![]() theo tĆnh chįŗ„t 4
theo tĆnh chįŗ„t 4![]() theo tĆnh chįŗ„t 1
theo tĆnh chįŗ„t 1![]() theo
tĆnh chįŗ„t 3
theo
tĆnh chįŗ„t 3![]() theo tĆnh chįŗ„t 2
theo tĆnh chįŗ„t 2![]() theo tĆnh chįŗ„t 4
theo tĆnh chįŗ„t 4![]() theo tĆnh chįŗ„t 1
theo tĆnh chįŗ„t 1![]() theo
tĆnh chįŗ„t 3
theo
tĆnh chįŗ„t 3![]() theo tĆnh chįŗ„t 2
theo tĆnh chįŗ„t 2![]() theo tĆnh chįŗ„t 4
theo tĆnh chįŗ„t 4![]() theo tĆnh chįŗ„t 1
theo tĆnh chįŗ„t 1
O(log n) phĆ©p rĆŗt gį»n theo modulo. Mį»i phĆ©p cĆ³ thį» thį»±c
hiį»n trong thį»i gian O((log n)2). Äiį»u ÄĆ³ chį»©ng tį» rįŗ±ng, Äį» phį»©c tįŗ”p
lĆ O((log n)3) lĆ Äa thį»©c theo log n. Thį»±c ra bįŗ±ng cĆ”c phĆ¢n tĆch
chĆnh xĆ”c hĘ”n, cĆ³ thį» chį»©ng tį» rÄng, Äį» phį»©c tįŗ”p chį» cį»” O((log n)2).
Giįŗ£ sį» ta ÄĆ£ tįŗ”o ÄĘ°į»£c mį»t sį»
ngįŗ«u nhiĆŖn n vĆ ÄĆ£ kiį»m tra tĆnh nguyĆŖn tį» cį»§a nĆ³ theo thuįŗt toĆ”n Soloway-
Strasen. Nįŗæu chįŗ”y thuįŗt toĆ”n m lįŗ§n thƬ cĆ¢u trįŗ£ lį»i n lĆ mį»t sį» nguyĆŖn tį» sįŗ½
cĆ³ mį»©c Äį» tin cįŗy nhĘ° thįŗæ nĆ o? Quįŗ£ lĆ liį»u lÄ©nh nįŗæu coi rÄng, xĆ”c suįŗ„t nĆ y lĆ
1-2-m. Kįŗæt luįŗn nĆ y thĘ°į»ng ÄĘ°į»£c nĆŖu trong cĆ”c giĆ”o trƬnh vĆ bĆ i bĆ”o
kÄ© thuįŗt, tuy nhiĆŖn ta khĆ“ng thį» dįŗ«n ra theo cĆ”c sį» liį»u cho trĘ°į»c.
Cįŗ§n phįŗ£i thįŗn trį»ng hĘ”n khi
sį»± dį»„ng cĆ”c tĆnh toĆ”n xĆ”c suįŗ„t. Ta sįŗ½
Äį»nh nghÄ©a cĆ”c biįŗæn ngįŗ«u nhiĆŖn sau:
a- Chį»
sį»± kiį»n sį» nguyĆŖn lįŗ» n cĆ³ kĆch thĘ°į»c ÄĆ£ Äį»nh lĆ mį»t hį»£p sį».
b- Chį»
sį»± kiį»n thuįŗt toĆ”n trįŗ£ lį»i n lĆ sį» nguyĆŖn tį» m lįŗ§n liĆŖn tiįŗæp .
Äiį»u chįŗÆc chįŗÆn lĆ prob(b| a)2-m.
Tuy nhiĆŖn xĆ”c suįŗ„t mĆ ta thį»±c sį»± quan tĆ¢m lĆ prob(a/b), xĆ”c suįŗ„t nĆ y thĘ°į»ng
khĆ“ng giį»ng nhĘ° prob(b/a).
CĆ³ thį» tĆnh prob(a/b) bįŗ±ng Äį»nh lĆ½ Bayes (Äį»nh lĆ½2.1).
TrĘ°į»c hįŗæt cįŗ§n phįŗ£i biįŗæt prob(a). Giįŗ£ sį» N Ć n Ć 2N. Ć”p
dį»„ng Äį»nh lĆ½ vį» sį» nguyĆŖn tį»: cĆ”c sį» nguyĆŖn tį»(lįŗ») giį»a N vĆ 2N xįŗ„p xį» bįŗ±ng:
2N/ln
2N N/ln N įŗ± N/ ln N
` įŗ± n/ln
n
VƬ cĆ³ N/2 įŗ± n/2
sį» nguyĆŖn tį» lįŗ» giį»a N vĆ 2N, ta sįŗ½ dĆ¹ng Ę°į»c lĘ°į»£ng
Prob(a) įŗ± 1
2/ln n
Sau ÄĆ³ cĆ³ thį» tĆnh toĆ”n nhĘ° sau:
prob(a| b) =
????
ChĆŗ Ć½ rįŗ±ng trong tĆnh toĆ”n trĆŖn ? chį» sį»± kiį»n sį» nguyĆŖn lįŗ» ngįŗ«u nhiĆŖn n lĆ mį»t sį» nguyĆŖn tį».
KhĆ” thĆŗ vį» nįŗæu so sĆ”nh hai hĆ m sau cį»§a
m
????/
Giįŗ£ sį»± n įŗ± 2256
įŗ± e177 (ÄĆ¢y
lĆ kĆch thĘ°į»c cį»§a cĆ”c sį» nguyĆŖn tį» sį»± dį»„ng trong hį» mįŗ·t RSA). Khi ÄĆ³ hĆ m Äįŗ§u
tiĆŖn xįŗ„p xį» bįŗ±ng????. Ta sįŗ½ lįŗp bįŗ£ng cho hai hĆ m į»©ng vį»i mį»t sį» giĆ” trį» cį»§a m
(xem hƬnh4.8).
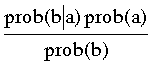
HƬnh 4.8. CĆ”c xĆ”c suįŗ„t sai Äį»i vį»i phĆ©p kiį»m tra
Solovay- Strasen
|
M |
2-m |
|
|
1 |
0,500 |
0,978 |
|
2 |
0250, |
0,956 |
|
5 |
0,312.10-1 |
0,732 |
|
10 |
0,977.10-3 |
0,787.10- |
|
20 |
0,954.10-6 |
0,834.10-4 |
|
30 |
0,930.10-9 |
0,815.10-7 |
|
50 |
0,888.10-15 |
0,777.10-13 |
|
100 |
0,789.10-30 |
0,690.10-28 |
Mįŗ·c dĆ¹????? tiįŗæn tį»i o khĆ” nhanh theo hĆ m mÅ© nhĘ°ng vįŗ«n
khĆ“ng tiįŗæn nhanh bįŗ±ng 2-m. Tuy nhiĆŖn, nįŗæu lįŗ„y m vĆ o cį»” 50 hoįŗ·c 100
thƬ cĆ”c xĆ”c suįŗ„t sai ÄĆ³ cĆ¹ng qui vį» mį»t lĘ°į»£ng rįŗ„t nhį».
Phįŗ§n nĆ y sįŗ½
kįŗæt thĆŗc bįŗ±ng mį»t thuįŗt toĆ”n Monte- Carlo khĆ”c cho bĆ i toĆ”n hį»£p sį», ÄĆ³ lĆ thuįŗt
toĆ”n Miller- Rabin (M-R) (ÄĘ°į»£c coi lĆ mį»t phĆ©p kiį»m tra giįŗ£ nguyĆŖn tį» mįŗ”nh).
Thuįŗt toĆ”n ÄĘ°į»£c mĆ“ tįŗ£ trong hƬnh 4.9. ÄĆ¢y lĆ” mį»t thuįŗt toĆ”n vį»i thį»i gian Äa
thį»©c: Äį» phį»©c tįŗ”p cį»§a nĆ³ cį»” O((log n)3) tĘ°Ę”ng tį»± nhĘ° thuįŗt toĆ”n S-S
Thį»±c ra trong thį»©c tįŗæ thuįŗt toĆ”n M-R thį»±c hiį»n tį»t hĘ”n thuįŗt toĆ”n S-S.
BĆ¢y giį» chĆŗng ta sįŗ½ chį» ra rįŗ±ng thuįŗt toĆ”n nĆ y khĆ“ng
thį» lį»i n lĆ mį»t hį»£p sį»
nįŗæu n lĆ sį» nguyĆŖn tį», tį»©c nĆ³ lĆ mį»t thuįŗt toĆ”n Äį»nh
hĘ°į»ng cĆ³ .
Äį»nh lĆ½ 4.10
thuįŗt toĆ”n Miller Rabin vį» cĆ”c hį»£p sį» lĆ thuįŗt
toĆ”n monte-carlo Äį»nh hĘ°į»ng cĆ³
HƬnh 4.9 Thuįŗt toĆ”n kiį»m tra tĆnh nguyĆŖn tį»
Miller-rabin vį»i sį» nguyĆŖn lįŗ» n
|
1. Viįŗæt
n-1=2km, trong ÄĆ³ m lĆ mį»t sį» lįŗ» 2. Chį»n
sį» nguyĆŖn ngįŗ«u nhiĆŖn a, 1 Ć a Ć
(n-1 ) 3.
TĆnh b=am mod n 4.
IF bŗ1
(mod n) then Trįŗ£
lį»i n lĆ sį» nguyĆŖn tį» vĆ quit 5.
For I=0 to
k-1 do 6. IF
bŗ-1
(mod n) then
Trįŗ£ lį»i n lĆ sį» nguyĆŖn tį» vĆ quit
Else b=b2 mod n 7.Trįŗ£
lį»i n lĆ hį»£p sį» |
Chį»©ng minh:
![]() Ta sįŗ½ chį»©ng minh bįŗ±ng cĆ”ch giįŗ£ sį»
thuįŗt toĆ”n trįŗ£ lį»i n lĆ hį»£p sį» vį»i sį»
nguyĆŖn tį» n nĆ o ÄĆ³ vĆ nhĆ¢n ÄĘ°į»£c mĆ¢u thuįŗ«t. VƬ thuįŗt toĆ”n trįŗ£ lį»i nlĆ hį»£ sį» nĆŖn chįŗÆc chįŗÆn lĆ am
ŗ 1(mod n). BĆ¢y giį» xĆ©t
dĆ£y cĆ”c giĆ” trį» b ÄĘ°į»£c kiį»m tra trong bĘ°į»c 2 cį»§a thuįŗt toĆ”n .VƬ b ÄĘ°į»£c bƬnh
phĘ°Ę”ng trong mį»i phĆ©p lįŗ·p cį»§a vĆ²ng For
nĆŖn ta sįŗ½ kiį»m tra cĆ”c giĆ” trį» am , a2m ,įŗ³,a2k-1m. VƬ thuįŗt
toĆ”n trįŗ£ lį»i n lĆ hį»£p sį» nĆŖn suy ra:
Ta sįŗ½ chį»©ng minh bįŗ±ng cĆ”ch giįŗ£ sį»
thuįŗt toĆ”n trįŗ£ lį»i n lĆ hį»£p sį» vį»i sį»
nguyĆŖn tį» n nĆ o ÄĆ³ vĆ nhĆ¢n ÄĘ°į»£c mĆ¢u thuįŗ«t. VƬ thuįŗt toĆ”n trįŗ£ lį»i nlĆ hį»£ sį» nĆŖn chįŗÆc chįŗÆn lĆ am
ŗ 1(mod n). BĆ¢y giį» xĆ©t
dĆ£y cĆ”c giĆ” trį» b ÄĘ°į»£c kiį»m tra trong bĘ°į»c 2 cį»§a thuįŗt toĆ”n .VƬ b ÄĘ°į»£c bƬnh
phĘ°Ę”ng trong mį»i phĆ©p lįŗ·p cį»§a vĆ²ng For
nĆŖn ta sįŗ½ kiį»m tra cĆ”c giĆ” trį» am , a2m ,įŗ³,a2k-1m. VƬ thuįŗt
toĆ”n trįŗ£ lį»i n lĆ hį»£p sį» nĆŖn suy ra:
![]() A2m
ŗ -1 (mod n)
A2m
ŗ -1 (mod n)
Vį»i 0 Ć i Ć k-1
BĆ¢y giį» sį»
dį»„ng giįŗ£ thiįŗæt n lĆ sį» nguyĆŖn tį». Theo Äį»nh lĆ½ Ferma (hį» quįŗ£ 4.6) ta cĆ³
A2km
ŗ 1 (mod 1)
VƬ n-1 = 2km. Khi ÄĆ³ a2k-1m lĆ
cÄn bįŗc hai cį»§a mį»t modulo n = ± 1
mod n. Äiį»u nĆ y cĆ³ thį» thįŗ„y rƵ nhĘ° sau: x lĆ cÄn bįŗc hai cį»§a 1 theo modulo n
khi vĆ chį» khi
nįŗµ(x-1)(x+1)
VƬ n lĆ mį»t sį» nguyĆŖn tį» nĆŖn hoįŗ·c nįŗµ(x-1)(tį»©c lĆ xŗ1 modun) hoįŗ·c nįŗµ(x+1) (tį»©c lĆ xŗ-1 modun)
Ta ÄĆ£ cĆ³
![]() a2k-1m ŗ
-1(mod n)
a2k-1m ŗ
-1(mod n)
bį»i vįŗy ta phįŗ£i cĆ³:
a2k-1m
ŗ 1(mod n)
Khi ÄĆ³ a2k-2m phįŗ£i lĆ cÄn bįŗc hai cį»§a 1.
Bįŗ±ng lįŗp luįŗn tĘ°Ę”ng tį»±:
A2k-1m
ŗ 1(mod n)
Äiį»u nĆ y lĆ mĆ¢u thuįŗ«n, bį»i vįŗy trong trĘ°į»ng hį»£p nĆ y
thuįŗt toĆ”n phįŗ£i cĆ³ cĆ¢u trįŗ£ lį»i n lĆ sį»
nguyĆŖn tį».;
CĆ²n mį»t vįŗ„n
Äį» chĘ°a chĘ°a ÄĘ°į»£c xem xĆ©t lĆ xĆ”c xuįŗ„t sai cį»§a thuįŗt toĆ”n M-R. Mįŗ·c dĆ¹ khĆ“ng
chį»©ng minh į» ÄĆ¢y nhĘ°ng cĆ³ thį» chį»©ng tį» ÄĘ°į»£c rįŗ±ng xĆ”c xuįŗ„t nĆ y nhiį»u nhįŗ„t lĆ
1/4.
![]()
4.6 CƔc phʰʔng
phĆ”p tįŗ„n cĆ“ng hį» mįŗt rsa
Trong phįŗ§n nĆ y ta sįŗ½ lĘ°u tĆ¢m
Äįŗæn vįŗ„n Äį»:Liį»u cĆ³ cĆ”c phĘ°Ę”ng phĆ”p tįŗ„n cĆ“ng RSA khĆ”c vį»i phĘ°Ę”ng phĆ”p phĆ¢n tĆch
n khĆ“ng ? trĘ°į»c tiĆŖn ta thįŗ„y rįŗ±ng thĆ”m mĆ£ chį» cįŗ§n tĆnh ÄĘ°į»£c F(n) lĆ Äį»§. Nįŗæu ÄĆ£ biįŗæt n vĆ F(n) vĆ n lĆ tĆch cį»§a 2 sį»
nguyĆŖn tį» p vĆ q thƬ cĆ³ thį» dį»
dĆ ng phĆ¢n tĆch ÄĘ°į»£c n bįŗ±ng cĆ”ch giįŗ£i 2 phĘ°Ę”ng
trƬnh sau Äį» tƬm hai sį» p vĆ q chĘ°a biįŗæt:
n=pq
F(n)=(p-1)(q-1)
Nįŗæu thay q=n/p vĆ phĘ°Ę”ng trƬnh thį»© 2 thƬ ta sįŗ½ thu ÄĘ°į»£c
phĘ°Ę”ng trƬnh bįŗc 2 cį»§a biįŗæn chĘ°a biįŗæt p :
P2-(n-F(n) + 1)p + n=0
Hai nghiį»m cį»§a phĘ°Ę”ng trƬnh nĆ y lĆ p vĆ
q lĆ cĆ”c nhĆ¢n tį»Æ cį»§a n. Bį»i vįŗy thĆ”m mĆ£ biįŗæt ÄĘ°į»£c F(n) thƬ anh ta cĆ³ thį» phĆ¢n
tĆch ÄĘ°į»£c n vĆ phĆ” ÄĘ°į»£c hį» mįŗt.NĆ³i cĆ”ch khĆ”c, viį»c tĆnh F(n) khĆ“ng dį»
hĘ”n viį»c phĆ¢n
tĆch n.Sau ÄĆ¢y lĆ mį»t vĆ dį»„ dį»„ minh hoįŗ” :
VĆ dį»„ 4.9
Giįŗ£ sį»
thĆ”m mĆ£ Äįŗ£ biįŗæt rįŗ±ng n=84773093 vĆ F(n)=
4754668. ThĆ“ng tin nĆ y sįŗ½ dįŗ«n tį»i phĘ°Ę”ng trƬnh:
P2-18426p+84773093=0
Giįŗ£i phĘ°Ę”ng trƬnh nĆ y thu
ÄĘ°į»£c hai nghiį»m 9539 vĆ 8887.ÄĆ¢y lĆ hai thį»«a sį» cį»§a n.;
4.6.1
Sį»
mÅ© giįŗ£i mĆ£
BĆ¢y giį» chĆŗng ta sįŗ½ chį»©ng minh
mį»t kįŗæt quįŗ£ rįŗ„t thĆŗ vį» lĆ mį»t thuįŗt toĆ”n bįŗ„t kį»³ Äį» tĆnh sį» mÅ© giįŗ£i mĆ£ a Äį»u cĆ³
thį» ÄĘ°į»£c dĆ¹ng nhĘ° mį»t chĘ°Ę”ng trƬnh con (hay mį»t Äiį»u kiį»n )trong thuįŗt toĆ”n xĆ”c
suįŗ„t phĆ¢n tĆch n .Bį»i vįŗy viį»c tĆnh a sįŗ½ khĆ“ng dį»
hĘ”n viį»c phĆ¢n tĆch n.Tuy
nhiĆŖn, cĆ³ mį»t Äiį»u khĆ“ng ngoĆ i quy luįŗt lĆ ta vįŗ«n cĆ³ thį» phĆ” hį» mįŗt mĆ khĆ“ng
cįŗ§n tĆnh a.
Kįŗæt quįŗ£ nĆ y cĆ³ Ć½ nghÄ©a nhiį»u hĘ”n vį» mįŗ·t lĆ½ thuyįŗæt .NĆ³
cho thįŗ„y rįŗ±ng nįŗæu a bį» lį» thƬ giĆ” trį» m cÅ©ng khĆ“ng cĆ²n khĆ³ phĆ¢n tĆch nį»Æa.Nįŗæu
Äiį»u nĆ y xįŗ©y ra thƬ viį»c Bob chį»n mį»t sį» mÅ© mį»i cÅ©ng chįŗ³ng cĆ³ Ć½ nghÄ©a; Äiį»u cįŗ§n
thiįŗæt lĆ Bob phįŗ£i chį»n lįŗ”i n.
Thuįŗt toĆ”n mĆ ta sįŗ½ mĆ“ tįŗ£ lĆ
mį»t thuįŗt toĆ”n xĆ”c suįŗ„t kiį»u las vegas.Sau ÄĆ¢y lĆ Äį»nh nghÄ©a cį»§a kiį»u thuįŗt
toĆ”n nĆ y.
Äį»nh nghÄ©a 4.5
Giįŗ£ sį» 0 Ć e Ć1 lĆ mį»t sį» thį»±c.Thuįŗt toĆ”n
las vegas lĆ mį»t thuįŗt toĆ”n xĆ”c suįŗ„t cao cho vį»i mį»t trĘ°į»ng hį»£p bįŗ„t kį»³ cį»§a bĆ i
toĆ”n I, thuįŗt toĆ”n cĆ³ thį» khĆ“ng cho kįŗæt quįŗ£ vį»i mį»t xĆ”c suįŗ„t e nĆ o
ÄĆ³ (chįŗ³ng hįŗ”n thuįŗt toĆ”n cĆ³ thį» kįŗæt thĆŗc vį»i thĆ“ng bĆ”o khĆ“ng trįŗ£ lį»i).Tuy
nhiĆŖn, nįŗæu thuįŗt toĆ”n cho lį»i giįŗ£i thƬ lį»i giįŗ£i nĆ y lĆ ÄĆŗng .
NhĆ¢n xĆ©t:Thuįŗt toĆ”n las vegas
cĆ³ thį» khĆ“ng cho cĆ¢u trįŗ£ lį»i nhĘ°ng mį»t cĆ¢u trįŗ£ lį»i bįŗ„t kį»³ mĆ thuįŗt toĆ”n cho lĆ
Äį»u lĆ cĆ¢u tra lį»i ÄĆŗng.NgĘ°į»£c lįŗ”i, thuįŗt toĆ”n monte-carlo luĆ“n luĆ“n cho cĆ¢u trįŗ£
lį»i nhĘ°ng cĆ¢u trĆ lį»i nĆ y cĆ³ thį» lĆ sai.
Nįŗæu
ta cĆ³ mį»t thuįŗt toĆ”n las vegas Äį» giįŗ£i mį»t bĆ i toĆ”n thƬ ÄĘ”n giįŗ£n ta chį» chįŗ”y
lįŗ·p Äi lįŗ·p lįŗ”i thuįŗt toĆ”n nĆ y cho tį»i khi nĆ³ tƬm ra mį»t cĆ¢u trįŗ£ lį»i.XĆ”c suįŗ„t Äį»
thuįŗt toĆ”n khĆ“ng trįŗ£ lį»i sau m lįŗ§n liĆŖn tiįŗæp lĆ em.Sį»
lįŗ§n chįŗ”y trung bƬnh Äį» thu ÄĘ°į»£c cĆ¢u tra lį»i thį»±c tįŗæ lĆ 1/e (Xem cĆ”c bĆ i tįŗp ).
Giįŗ£ sį» A lĆ mį»t thuįŗt toĆ”n giįŗ£ Äį»nh tĆnh
sį» mÅ© giįŗ£i mĆ£ a tį»« b. Ta sįŗ½ mĆ“ tįŗ£ mį»t thuįŗt toĆ”n las vegas dĆ¹ng A nhĘ° mį»t
chĘ°Ę”ng trƬnh giįŗ£ Äį»nh (oracle) con.Thuįŗt toĆ”n sįŗ» phĆ¢n tĆch n vį»i xĆ”c suįŗ„t tį»i
thiį»u lĆ 1/2.Bį»i vįŗy nįŗæu thuįŗt toĆ”n chįŗ”y m lįŗ§n thƬ n sįŗ½ ÄĘ°į»£c phĆ¢n tĆch vį»i xĆ”c
suįŗ„t tį»i thiį»u lĆ 1-1/2m.
Thuįŗt
toĆ”n ÄĘ°į»£c xĆ¢y dį»±ng trĆŖn cĘ” sį» mį»t sį» nguyĆŖn tį» nhįŗ„t Äį»nh liĆŖn quan tį»i cĆ”c cÄn
bįŗc 2 cį»§a mį»t theo modulo n, trong ÄĆ³
n=pq lĆ tĆch cį»§a hai sį» nguyĆŖn tį» lįŗ» phĆ¢n biį»t ta biįŗæt rįŗ±ng phĘ°Ę”ng trƬnh Äį»ng
dĘ° X2 ŗ1( mod p) cĆ³ hai nghiį»m theo
modulo p lĆ X=±1 mod p .TĘ°Ę”ng tį»±,
phĘ°Ę”ng trƬnh Äį»ng dĘ° X2ŗ1(mod
q) cÅ©ng cĆ³ hai nghiį»m lĆ X=±1 mod
q .
VƬ X2 ŗ1 (mod n) khi vĆ chį» khi X2ŗ1 (mod p) vĆ X2ŗ1 (mod q) nĆŖn suy ra X2ŗ 1 (mod n) khi vĆ chį» khi X=±1 mod p vĆ X=±1 mod q.Bį»i vįŗy cĆ³ 4 cÄn bįŗc
2 cį»§a 1 theo modulo n vĆ cĆ”c cÄn nĆ y cĆ³ thį» tƬm ÄĘ°į»£c thĆ“ng qua Äį»nh lĆ½ phįŗ§n dĘ°
china.Hai trong cĆ”c nghiį»m nĆ y lĆ X=±1 mod
n; chĆŗng ÄĘ°į»£c gį»i lĆ cĆ”c cÄn bįŗc hai tįŗ§m thĘ°į»ng vĆ lĆ cĆ”c giĆ” trį» Äį»i cį»§a nhau
theo modulo n.
Sau ÄĆ¢y lĆ mį»t vĆ dį»„ dį»„ nhį» Äį» minh hoįŗ”
:
VĆ dį»„ 4.10
Giįŗ£
sį» n=403=13 *11.Bį»n cÄn bįŗc hai cį»§a
mį»t theo modulo 403 lĆ 1,92,311 vĆ 402.CÄn bįŗc hai 92 nhįŗn ÄĘ°į»£c bįŗ±ng cĆ”ch giįŗ£i
hį» Xŗ1 (mod 13) , Xŗ-1 (mod 31) theo Äį»nh lĆ½ phįŗ§n
dĘ° china.Nįŗæu tƬm ÄĘ°į»£c khĆ“ng tįŗ§m thĘ°į»ng
nĆ y, nghiį»m khĆ“ng tįŗ§m thĘ°į»ng kia phįŗ£i lĆ 403-92=311.ÄĆ³ lĆ nghiį»m cį»§a hį» Xŗ-1(mod 13), Xŗ1 (mod 31).
Giįŗ£
sį» X lĆ cÄn bįŗc hai khĆ“ng tįŗ§m thĘ°į»ng cį»§a 1 modulo n. Khi ÄĆ³ ta cĆ³
nįŗµ(x-1)(x+1)
nhĘ°ng n khĆ“ng lĆ Ę°į»c cį»§a mį»t nhĆ¢n tį» nĆ o į» vįŗæ phįŗ£i
.Äiį»u ÄĆ³ kĆ©o theo UCLN (X+1,n) = p hoįŗ·c q(vĆ tĘ°Ę”ng tį»± UCLN(X-1,n)=p hoįŗ·c q).Tįŗ„t
nhiĆŖn cĆ³ thį» tĆnh UCLN bįŗ±ng thuįŗt toĆ”n Euclide mĆ khĆ“ng cįŗ§n phįŗ£i biįŗæt phĆ¢n tĆch
nhĆ¢n tį» cį»§a n.Bį»i vįŗy, hiį»u biįŗæt vį» cÄn bįŗc hai khĆ“ng tįŗ§m thĘ°į»ng cį»§a 1 mod n sįŗ½
lĆ m cho viį»c phĆ¢n tĆch n chį» cįŗ§n thį»±c hiį»n trong thį»i gian Äa thį»©c.
Trong vĆ dį»„ dį»„ 4.10 į» trĆŖn, UCLN (93,403) =31 vĆ UCLN
(312,403)=13
TrĆŖn hƬnh 4.10 trƬnh bĆ y thuįŗt toĆ”n (dĆ¹ng thuįŗt toĆ”n
giįŗ£ Äį»nh A lĆ m chĘ°Ę”ng trƬnh con) Äį» phĆ¢n tĆch n bįŗ±ng cĆ”ch tƬm mį»t cÄn bįŗc hai
khĆ“ng tįŗ§m thĘ°į»ng cį»§a 1 modulo n (A thį»±c hiį»n tĆnh sį» mÅ© giįŗ£i mĆ£ a theo sį» mÅ© mĆ£
b ).TrĘ°į»c tiĆŖn ta sįŗ½ ÄĘ°a ra mį»t vĆ dį»„ Äį» minh hoįŗ” cho viį»c Ć”p dį»„ng thuįŗt toĆ”n
nĆ y.
vĆ dį»„ 4.11
Giįŗ£ sį» n=89855713, b=34986517
vĆ a=82330933 vĆ giĆ” trį» ngįŗ«u nhiĆŖn w=5.Ta cĆ³ :
ab-1=23.360059073378795
trong bĘ°į»c 6, v=85877701 cĆ²n į» bĘ°į»c 10 , v=1.Trong bĘ°į»c
12 ta tĆnh
UCLN
(85877702,n)=9103.
ÄĆ¢y lĆ mį»t thį»«a sį» cį»§a n; thį»«a sį» kia lĆ n/9103=9871.
BĆ¢y giį» sįŗ½ tiįŗæn hĆ nh phĆ¢n
tĆch thuįŗt toĆ”n.TrĘ°į»c tiĆŖn, nhĆ¢n thįŗ„y rįŗ±ng nįŗæu ta may mįŗÆn chį»n ÄĘ°į»£c w lĆ bį»i
cį»§a p hoįŗ·c q thƬ cĆ³ thį» ngay lįŗp tį»©c phĆ¢n tĆch ÄĘ°į»£c n.Äiį»u nĆ y ÄĘ°į»£c biį»u thį» į»
bĘ°į»c 2. Nįŗæu Ę° nguyĆŖn tį» cĆ¹ng nhau vį»i n thƬ chĆŗng ta sįŗ½ tĆnh wr , w2r,
w4r,
,Bįŗ±ng cĆ”ch bƬnh phĘ°Ę”ng liį»n tiįŗæp cho tį»i khi
W2r
ŗ1 (mod n)
Vį»i giĆ” trį» t nĆ o ÄĆ³.VƬ
Ab-1=2srŗ0 (mod F(n))
HƬnh 4.10 Thuįŗt toĆ”n phĆ¢n tĆch thį»«a sį» (cho trĘ°į»c sį» mÅ©
giįŗ£i mĆ£ a).
|
1.
2.
TĆnh x=UCLN(w,n) 3.
IF 1 < x < n then quit (thĆ nh cĆ“ng :x=p
hoįŗ·c x=q) 4.
TĆnh a=A(b) 5.
Viįŗæt ab-1=2sr, r Lį»£ 6.
TĆnh v=wr mod n 7.
IF v=1 (mod n) then quit (khĆ“ng thĆ mh cĆ“ng) 8.
While v
ŗ 1 (mod n) do 9.
V0=v 10.
v=v2 mod n 11.
If v0
ŗ-1 (mod n) then Quit (khĆ“ng thĆ nh cĆ“ g) Else TĆnh x=UCLN(v0+1,n)
(thĆ nh cĆ“ng :x=p hoįŗ·c x=q) |
![]() Nįŗæu ta cĆ³ W2rŗ1(mod n) .Bį»i vįŗy, vĆ²ng lįŗ·p
while sįŗ½ kįŗæt thĆŗc sau nhiį»u nhįŗ„t lĆ s bĘ°į»c lįŗ·p .kįŗæt thĆŗc vĆ²ng lįŗ·p, ta tƬm ÄĘ°į»£c
mį»t giĆ” trį» v0 sao cho v02ŗ1 (mod n) nhĘ°ng
v0ŗ 1
(mod n) .Nįŗæu v0ŗ-1
(mod ,n ) thƬ thuįŗt toĆ”n khĆ“ng thĆ nh cĆ“ng ; ngĘ°į»£c lįŗ”i , v0 sįŗ½ lĆ
mį»t cÄn bįŗc hai khĆ“ng tįŗ§m thĘ°į»ng cį»§a 1
modulo n vĆ ta phĆ¢n tĆch ÄĘ°į»£c n (bĘ°į»c 12
).
Nįŗæu ta cĆ³ W2rŗ1(mod n) .Bį»i vįŗy, vĆ²ng lįŗ·p
while sįŗ½ kįŗæt thĆŗc sau nhiį»u nhįŗ„t lĆ s bĘ°į»c lįŗ·p .kįŗæt thĆŗc vĆ²ng lįŗ·p, ta tƬm ÄĘ°į»£c
mį»t giĆ” trį» v0 sao cho v02ŗ1 (mod n) nhĘ°ng
v0ŗ 1
(mod n) .Nįŗæu v0ŗ-1
(mod ,n ) thƬ thuįŗt toĆ”n khĆ“ng thĆ nh cĆ“ng ; ngĘ°į»£c lįŗ”i , v0 sįŗ½ lĆ
mį»t cÄn bįŗc hai khĆ“ng tįŗ§m thĘ°į»ng cį»§a 1
modulo n vĆ ta phĆ¢n tĆch ÄĘ°į»£c n (bĘ°į»c 12
).
Nhiį»m vį»„ chĆnh cĆ²n lįŗ”i bĆ¢y giį» lĆ phįŗ£i chį»©ng minh rįŗ±ng,
thuįŗt toĆ”n thĆ nh cĆ“ng vį»i xĆ”c suįŗ„t lĆ įŗµ .CĆ³ hai cĆ”ch mĆ theo ÄĆ³ thuįŗt toĆ”n cĆ³
thį» khĆ“ng thĆ nh cĆ“ng khi phĆ¢n tĆch n :
1.Wrŗ1 (mod n) (bĘ°į»c 7)
2.W2rŗ-1 ( mod n ) vį»i giĆ” trį» t nĆ o ÄĆ³ , 0 Ć t Ć s-1 (bĘ°į»c 11)
ChĆŗng ta cĆ³ n+1 phĘ°Ę”ng trƬnh
Äį»ng dĘ° Äį» xem xĆ©t.Nįŗæu giĆ” trį» ngįŗ«u nhiĆŖn w lĆ mį»t nghiį»m cį»§a Ćt nhįŗ„t mį»t trong
cĆ”c Äį»ng dĘ° thį»©c nĆ y thƬ phĆ©p lį»±a chį»n w nĆ y lĆ tį»i vĆ thuįŗt toĆ”n sįŗ½ khĆ“ng
thĆ nh cĆ“ng. Bį»i vįŗy, ta sįŗ½ chuyį»n sang tĆnh sį» cĆ”c nghiį»m cį»§a mį»i ÄĆ“ng dĘ° thį»©c
nĆ y.
TrĘ°į»c tiĆŖn xĆ©t Äį»ng dĘ° thį»©c wrŗ1 (md n). PhĘ°Ę”ng phĆ”p phĆ¢n tĆch mį»t Äį»ng dĘ° thį»©c giį»ng
nhĘ° cĆ”ch xem xĆ©t mį»t cĆ”ch riĆŖng rįŗ» cĆ”c nghiį»m theo modulo q. Sau ÄĆ³ kįŗæt hį»£p
chĆŗng nhį» Äį»nh lĆ½ phįŗ§n dĘ° China. Cįŗ§n Äį» Ć½ rįŗ±ng xŗ1
(mod n) khi vĆ chį» khi xŗ1
(mod p) vĆ xŗ1 (mod q).
NhĘ° vįŗy,
trĘ°į»c hįŗæt ta phįŗ£i xĆ©t wrŗ1
(mod n). VƬ p lĆ mį»t sį» nguyĆŖn tį» nĆŖn Zp* lĆ mį»t nhĆ³m
cyclic theo Äį»nh lĆ½ 4.7. Giįŗ£ sį» g lĆ mį»t phįŗ§n tį» nguyĆŖn thuį»· theo modulo p. Ta
cĆ³ thį» viįŗæt w=gu vį»i sį» nguyĆŖn duy nhįŗ„t u nĆ o ÄĆ³, 0 Ć u Ć p-2. Khi ÄĆ³ ta cĆ³ :
Wr ŗ1(mod
p)
gurŗ1
(mod p)
(p-1) įŗµur
Giįŗ£ sį» ta
biį»u diį»
n p-1=2ip1 trong ÄĆ³ p1 lĆ mį»t sį» lįŗ» vĆ
q-1 =2jq1, q1 lĆ mį»t sį» lįŗ».
VƬ
F(n)=(p-1)(q-1) įŗµ(ab-1)=2sr
nĆŖn ta cĆ³
2i+jp1q1įŗµ2sr
Bį»i vįŗy:
i+j Ć s
VĆ
P1q1įŗµ r
BĆ¢y giį» Äiį»u kiį»n p-1 įŗµ ur sįŗ» trį» thĆ nh 2ip1
įŗµur. VƬ p1įŗµr vĆ r lįŗ» nĆŖn Äiį»u kiį»n cįŗ§n
vĆ Äį»§ lĆ 2iįŗµu.VƬ
thįŗæ, u=k. 2i, 0Ć k Ć p1-1 vĆ sį» cĆ”c
nghiį»m cį»§a dĘ° thį»©c wrŗ1
(mod p) sįŗ» lĆ p1.
Bįŗ±ng lįŗp
luįŗn tĘ°Ę”ng tĘ°, ta thįŗ„y Äį»ng dĘ° thį»©c wr ŗ1 (mod q) sįŗ» cĆ³ ÄĆŗng q1
nghiį»m.CĆ³ thį» kįŗæt hį»£p nghiį»m bįŗ„t kį»³ theo modulo p vį»i nghiį»m bįŗ„t kį»³ theo modulo
q Äį» thu ÄĘ°į»£c mį»t nghiį»m duy nhįŗ„t theo modulo n nhį» Äį»nh lĆ½ phįŗ§n dĘ° China. Do
vįŗy sį» cĆ”c nghiį»m cį»§a Äį»ng dĘ° thį»©c wrŗ1
(modn ) sįŗ» lĆ p1q1.
Tiįŗæp theo, xĆ©t Äį»ng dĘ° thį»©c w2r
ŗ1(mod n) vį»i giĆ” trį» t
cį» Äį»nh
(trong ÄĆ³ : 0 Ć t Ć s-1).
TrĘ°į»c
tiĆŖn lįŗ”i xĆ©t Äį»ng dĘ° thį»©c theo modulo p rį»i sau Äo xĆ©t theo modulo q. (Äį» Ć½
rįŗ±ng, ???ŗ-1 (mod n) khi vĆ chį»
khi w2rŗ-1 (mod p) vĆ
![]() . Äįŗ§u tiĆŖn ta xĆ©t
. Äįŗ§u tiĆŖn ta xĆ©t ![]() nįŗæu viįŗæt nhĘ° į» phįŗ§n
trĆŖn ta nhįŗn ÄĘ°į»£c
nįŗæu viįŗæt nhĘ° į» phįŗ§n
trĆŖn ta nhįŗn ÄĘ°į»£c ![]()
VƬ g(p-1)/2ŗ -1(mod
p) nĆŖn ta cĆ³
u2tr ŗ(p-1)/2( mod p-1)
(p-1) │ (u2tr-(p-1)/2)
2(p-1)│ (u2t+1r-(p-1))
VƬ p-1=2ip1 nĆŖn ta nhįŗn ÄĘ°į»£c
2i+2 p1 │ u 2t+1r-2ip1)
Loai
bį» thį»«a sį» chung ta cĆ³
2i+1 │ (u![]() -2i)
-2i)
XĆ©t
thįŗ„y nįŗæu ![]() thƬ cĆ³ thį» lĆ khĆ“ng cĆ³
nghiį»m do 2i+1 │ 2t+1 nhĘ°ng
thƬ cĆ³ thį» lĆ khĆ“ng cĆ³
nghiį»m do 2i+1 │ 2t+1 nhĘ°ng
2i+1 │ 2i
Mįŗ·t khĆ”c nįŗæu ![]() -1 thƬ u sįŗ½ lĆ mį»t
nghiį»m khi vĆ chį» khi u lĆ bį»i lįŗ» cį»§a 2i-t-1 .
-1 thƬ u sįŗ½ lĆ mį»t
nghiį»m khi vĆ chį» khi u lĆ bį»i lįŗ» cį»§a 2i-t-1 .
(chĆŗ
Ć½ rįŗ±ng r/p1 lĆ mį»t sį» nguyĆŖn lįŗ»). Bį»i vįŗy, sį» cĆ”c nghiį»m trong
trĘ°į»nh hį»£p nĆ y lĆ
![]() =2tp1
=2tp1
TĘ°Ę”ng tį»±, Äį»ng dĘ° thį»©c ![]() (mod q) sįŗ½ :
(mod q) sįŗ½ :
- KhĆ“ng cĆ³ nghiį»m nįŗæu ![]()
- CĆ³ 2tq1 nghiį»m nįŗæu t Ć j-1
Tį»«
Äį»nh lĆ½ phįŗ§n dĘ° China ta sįŗ½ thįŗ„y rįŗ±ng sį» cĆ”c nghiį»m cį»§a ![]() lĆ
lĆ
-
0 nįŗæu ![]()
-
22t p1q1 nįŗæu ![]()
t cĆ³
thį» nįŗ±m trong dįŗ£i tį»« 0 tį»i s-1. KhĆ“ng mįŗ„t tĆnh tį»nh quĆ”t giįŗ£ sį» i Ć j;
khi ÄĆ³ sį» cĆ”c nghiį»m sįŗ½ bįŗ±ng 0 nįŗæu ![]() . Tį»ng sį» cĆ”c lį»±a chį»ntį»i cį»§a w nhiį»u nhįŗ„t lĆ
. Tį»ng sį» cĆ”c lį»±a chį»ntį»i cį»§a w nhiį»u nhįŗ„t lĆ
p1q1+p1q1(1+22+24+įŗ³+22i-1) = pĘ°1q1(1+![]() )
)
=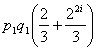
Äį» Ć½ lĆ p-1 = 2ip1 cĆ²n q-1=2jq1. BĆ¢y giį» giįŗ£ sį» j ³ i ³1 khi ÄĆ³ p1q1<n/4
Ta cÅ©ng cĆ³ :
22ip1q1
Ć 2i+j p1q1
=(p-1)(q-1) < n
Bį»i vįŗy:
p1q1(![]() )<
)<![]()
VƬ cĆ³ nhiį»u nhįŗ„t lĆ (n-1)/2 phĆ©p chį»n tį»i Äį»i vį»i w nĆŖn Äiį»u ÄĆ³ cĆ³ nghÄ©a lĆ cĆ³ Ćt nhįŗ„t (n-1)/2 phĆ©p chį»n tį»t vĆ vƬ thįŗæ xĆ”c suįŗ„t thĆ nh cĆ“ng cį»§a thuįŗt toĆ”n tį»i thiį»u lĆ 1/2.
4.6.2 .ThĆ“ng tin riĆŖng cĆ³ liĆŖn quan tį»i cĆ”c bit cį»a bįŗ£n rƵ
11111111111111
XĆ©t mį»t kįŗæt quįŗ£ khĆ”c cĆ³ liĆŖn
quan tį»i thĆ“ng tin vį» bįŗ£n rƵ cĆ³ thį» bį» rĆ² rį»
bį»i phĆ©p mĆ£ hoĆ” RSA. Sau ÄĆ¢y lĆ hai trĘ°į»ng hį»£p xĆ©t vį» thĆ“ng tin riĆŖng
1.
Cho y=eĘ°KĘ°(x), hĆ£y tĆnh parity(y)
trong ÄĆ³ parity(y) chį» bĆt cįŗ„p
thįŗ„p cį»§a x.
2.
Cho y=eK(x), hĆ£y tĆnh half(y) trong ÄĆ³ half(y)=0 nįŗæu ![]() vĆ half(y)=1 nĆ©u
vĆ half(y)=1 nĆ©u ![]()
Ta sįŗ½ chį»©ng minh rįŗ±ng vį»i y=eK(x)
cho trĘ°į»c mį»t thuįŗt toĆ”n bįŗ„t kį»³ tĆnh parity(y) hoįŗ·c half(y) Äį»u cĆ³ thį» ÄĘ°į»£c dĆ¹ng nhĘ° mį»t chĘ°Ę”ng trƬnh con Äį» xĆ¢y dį»±ng
mį»t thuįŗt toĆ”n tĆnh bįŗ£n x. Äiį»u ÄĆ³ cĆ³
nghÄ©a lĆ , vį»i mį»t bįŗ£n mĆ£ cho trĘ°į»c, viį»c tĆnh bit bįŗc thįŗ„p cį»§a bįŗ£n rƵ sįŗ½ tĘ°Ę”ng
ÄĘ°Ę”ng Äa thį»©c vį»i viį»c xĆ”c Äį»nh toĆ n bį» bįŗ£n rƵ !
TrĘ°į»c hįŗæt, ta sįŗ½ chį»©ng minh rįŗ±ng, viį»c tĆnh parity(y) lĆ tĘ°Ę”ng ÄĘ°Ę”ng Äa thį»©c vį»i viį»c tĆnh half (y). Äiį»u nĆ y rĆŗt ra tį»« hai Äį»ng nhįŗ„t thį»©c ÄĘ”n giįŗ£n sau (xĆ©t bĆ i tįŗp ):
halt(y)=parity(y x eK(2)
mod n) (4.1)
parity(y)=half(y x eK(2Ę°-1)mod n) (4.2)
vĆ tį»« quy tįŗÆc nhįŗn eK(x1)
eK(x2)=eK(x1x2)
Ta sįŗ½
chį» ra cĆ”ch tĆnh x=dK(y) theo mį»t thuįŗt toĆ”n giįŗ£ Äį»nh cho trĘ°į»c Äį»
tĆnh half(y). Thuįŗt toĆ”n ÄĘ°į»£c trƬnh bĆ y trĆŖn hƬnh 4.11 .Trong cĆ”c bĘ°į»c 2.4 ta
tĆnh :
yi = half(y x
(eK(2))I)=half(eK(x x2i))
vį»i ![]() . Nhįŗn thįŗ„y rįŗ±ng:
. Nhįŗn thįŗ„y rįŗ±ng:
half
(eK(x))= 0 ![]() x
x![]()
half(eK(2x)=0 ![]()
![]()
![]()
half(eK(4x))= 0 Ū ![]()
![]()
Bį»i
vįŗy ta cĆ³ thį» tƬm theo kį»¹ thuįŗt tƬm tƬm kiįŗæm nhį» phĆ¢n (ÄĘ°į»£c lĆ m trong cĆ”c bĘ°į»c
7-11). DĘ°į»i ÄĆ¢y lĆ mį»t vĆ dį»„ nhį» Äį» minh hoįŗ”
VĆ dį»„ 4.12
Giįŗ£
sį» n=1457, b=779 vĆ ta cĆ³ bįŗ£n mĆ£ y=772. eK(2) ÄĘ°į»£c tĆnh bįŗ±ng 946.
Giįŗ£ giį» rįŗ±ng (sį» dį»„ng thuįŗt toĆ”n giįŗ£ Äį»nh Äį»i vį»i half(y)) . ta nhįŗn ÄĘ°į»£c cĆ”c
giĆ” trį» yi sau theo bĘ°į»c 3 thuįŗt toĆ”n:
HƬnh 4.11.Giįŗ£ mĆ£ bįŗ£n mĆ£ RSA vį»i mį»t thuįŗt toĆ”n
giįŗ£ Äį»nh tĆnh
half(y) cho
trĘ°į»c
1.
KĆ½ hiį»u k=│log2 n │ 2.
For i=0 to k do 3.
yi =half(y) 4.
y=(y* eK(2))
mod 2 5.
lo=0 6.
hi=n 7.
for i=0 to k do 8.
mid=(hi+lo)/2 9.
IF yi=1 then lo=mid else hi=mid 10. x=│hi│
HƬnh
4.12. PhĆ©p tƬm kiįŗæm nhį» phĆ¢n Äį» giįŗ£i mĆ£ RSA.
|
I |
Lo |
Mid |
Hi |
|
0 |
0.00 |
728.50 |
1457.00 |
|
1 |
728.50 |
1092.75 |
1457.00 |
|
2 |
728.50 |
910.62 |
1092.75 |
|
3 |
910.62 |
1001.69 |
1092.75 |
|
4 |
910.62 |
956.16 |
1001.69 |
|
5 |
956.16 |
978.92 |
1001.69 |
|
6 |
978.92 |
990.00 |
1001.69 |
|
7 |
990.30 |
996.00 |
1001.69 |
|
8 |
996.00 |
998.84 |
1001.69 |
|
9 |
998.84 |
1000,26 |
1001.26 |
|
10 |
998.84 |
999.55 |
1000.26 |
|
|
998.84 |
999.25 |
999.55 |
i │0 │
1 │ 2 │ 3 │ 4 │ 5 │6 │
7 │ 8 │ 9 │ 10
yi │1 │ 0 │ 1 │ 0 │ 1 │
1│ 1 │ 1 │ 1 │ 0 │
0
Sau ÄĆ³ tiįŗæn hĆ nh tƬm kiįŗæm
nhį» phĆ¢n theo hƬnh 4.12. Bįŗ£n rƵ tƬm thįŗ„y lĆ x=│999.55│=999.
![]() Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°
Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°Ę°
4.7. Hį» MįŗT RABIN
Trong phįŗ§n nĆ y sįŗ½ mĆ“ tįŗ£ hį» ma trįŗn Rabin. ÄĆ¢y lĆ hį» mįŗt cĆ³ Äį» an toĆ n cao vį» mįŗ·t tĆnh toĆ”n chį»ng lįŗ”i ÄĘ°į»£c cĆ”ch tįŗ„n cĆ“ng bįŗ£n rƵ lį»±a chį»n vĆ khĆ“ng cĆ³ khįŗ£ nÄng phĆ¢n tĆch ÄĘ°į»£c n=pq(hį» ÄĘ°į»£c trƬnh bĆ y trong hƬnh 4.13).
ChĆŗng ta sįŗ½ chį» ra rįŗ±ng, hĆ m mĆ£ hoĆ” ek khĆ“ng phįŗ£i lĆ mį»t
ÄĘ”n Ć”nh, vƬ thįŗæ phĆ©p giįŗ£i mĆ£ khĆ“ng thį» thį»±c hiį»n ÄĘ°į»£c mį»t cĆ”ch xĆ”c Äį»nh. Thį»±c
tįŗæ cĆ³ 4 bįŗ£n rƵ cĆ³ thį» į»©ng vį»i mį»t bįŗ£n mĆ£ bįŗ„t kį»³ cho trĘ°į»c. ChĆnh xĆ”c hĘ”n, giįŗ£
sį» w lĆ mį»t trong 4 cÄn bįŗc hai cį»§a mį»t modulo n. Giįŗ£ sį» xє Zn. Khi ÄĆ³ cĆ³ thį»
kiį»m tra cĆ”c phĘ°Ę”ng trƬnh sau:
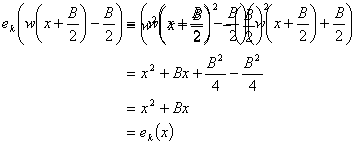
(Cįŗ§n chĆŗ Ć½
lĆ tįŗ„t cįŗ£ cĆ”c phĆ©p tĆnh sį» hį»c Äį»u thį»±c hiį»n trong Zn, cĆ²n phĆ©p chia
cho 2 vĆ 4 giį»ng nhĘ° phĆ©p nhĆ¢n 2-1vĆ 4-1 theo modulo n ).
HƬnh 4.13. Hį» mįŗt Rabin
Giįŗ£ sį» n lĆ tĆch cį»§a hai sį» nguyĆŖn tį» phĆ¢n biį»t p
vĆ q, p.q Ć
3 (mod 4). Giįŗ£ sį» p
=C=Zn vĆ ta xĆ”c Äį»nh K={(n
, p , q , B): 0 Ć B Ćn-1} Vį»i K = (n , p , q , B) ta Äį»nh nghÄ©a: ek(x)
= x( x+B) mod n vĆ cĆ”c giĆ” trį» n vĆ B ÄĘ°į»£c cĆ“ng khai trong khi p vĆ q
ÄĘ°į»£c giį»Æ kĆn.
![]()
Bį»n bįŗ£n rƵ mĆ£ hoĆ” thĆ nh eK(x) lĆ x, -x B, w(x+B/2) vĆ
-w(x+B/2), trong ÄĆ³ w lĆ mį»t cÄn bįŗc hai khĆ“ng tįŗ§m thĘ°į»ng cį»§a 1modulo n. NĆ³i
chung Bob khĆ“ng cĆ³ cĆ”ch nĆ o Äį» xĆ”c Äį»nh bįŗ£n nĆ o trong bį»n bįŗ£n rƵ cĆ³ thį» nĆ y lĆ bįŗ£n rƵ ÄĆŗng, trį»« phi
bįŗ£n rƵ cĆ³ Äį»§ Äį» dĘ° Äį» loįŗ”i bį» ba trong bį»n bįŗ£n rƵ ÄĆ³.
BĆ¢y giį» ta xem xet bĆ i toĆ”n giįŗ£i mĆ£ theo quan Äiį»m cį»§a Bob. Anh ta
ÄĆ£ cĆ³ bįŗ£n mĆ£ y vĆ muį»n xĆ”c Äį»nh x sao cho:
x2+ bx ŗ y(mod n)
ÄĆ¢y lĆ mį»t phĘ°Ę”ng trƬnh bįŗc hai theo giĆ” trį» x chĘ°a biįŗæt. Ta cĆ³ thį»
loįŗ”i bį» sį» hįŗ”ng tuyįŗæn tĆnh bįŗ±ng phĆ©p thįŗæ x1=x+B/2 (Hay x = x1-
B/2). Khi ÄĆ³ phĘ°Ę”ng trƬnh trĆŖn cĆ³ dįŗ”ng
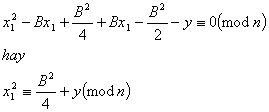
Nįŗæu Äįŗ·t![]() thƬ cĆ³ thį» viįŗæt lai phĘ°Ę”ng trƬnh Äį»ng dĘ° nhĘ° sau:
thƬ cĆ³ thį» viįŗæt lai phĘ°Ę”ng trƬnh Äį»ng dĘ° nhĘ° sau:
x1 ŗ C (mod n)
NhĘ° vįŗy phĆ©p giįŗ£i mĆ£ sįŗ½ chį» cĆ²n lĆ thį»±c hiį»n phĆ©p khai cÄn bįŗc hai theo modulo n. Äiį»u nĆ y tĘ°Ę”ng ÄĘ°Ę”ng vį»i viį»c giįŗ£i phĘ°Ę”ng trƬnh Äį»ng dĘ° sau:
x12 ŗ C (mod p)
x12
ŗ C (mod q)
(CĆ³ hai cÄn bįŗc hai cį»§a C modolo p vĆ hai cÄn bįŗc cį»§a C theo modolo
q. Bįŗ±ng cĆ”ch dĆ¹ng Äį»nh lĆ½ phįŗ§n dĘ° China, cĆ”c nghiį»m nĆ y cĆ³ thį» ÄĘ°į»£c kįŗæt hį»£p Äį»
tįŗ”o nĆŖn bį»n nghiį»m theo modulo n). CĆ³ thį» dĆ¹ng tiĆŖu chuįŗ©n Eucler Äį» xĆ”c Äį»nh
xem C cĆ³ phįŗ£i lĆ mį»t thįŗ·ng dĘ° bįŗc hai theo modulo p ( vĆ modulo q) hay khĆ“ng .
TrĆŖn thį»±c tįŗæ, C lĆ mį»t thįŗ·ng dĘ° bįŗc hai theo modulo p vĆ modulo q nįŗæu phĆ©p mĆ£
hoĆ” ÄĘ°į»£c thį»±c hiį»n ÄĆŗng. Tuy nhiĆŖn tiĆŖu chuįŗ©n Eucler khĆ“ng giĆŗp chĆŗng ta tƬm
ÄĘ°į»£c cĆ”c cÄn bįŗc hai cį»§a C. NĆ³ chį» ra mį»t cĆ¢u trįŗ£ lį»i CĆ³ hoÄc KhĆ“ng.
Khi p ŗ 3 (mod 4), ta cĆ³ mį»t cĆ“ng thį»©c ÄĘ”n giįŗ£n Äį» tĆnh cĆ”c cÄn bįŗc hai
cį»§a cĆ”c thįŗ·ng dĘ° bįŗc hai theo modulo p.
Giįŗ£ sį» C lĆ mį»t thįŗ·ng dĘ° bįŗc hai vĆ p ŗ 3 (mod 4) . Khi ÄĆ³ ta cĆ³:
(± C(p+1)/4)2
ŗ C(p+1)/2(mod
p)
ŗ C(p-1)/2
C (mod p)
ŗ C(mod p)
į» ÄĆ¢y ta lįŗ”i mį»t lįŗ§n nį»Æa sį» dį»„ng tiĆŖu
chuįŗ©n Eucler, hai tiĆŖu chuįŗ©n nĆ y phĆ”t biį»u rįŗ±ng, nįŗæu C lĆ mį»t thįŗ·ng dĘ° bįŗc hai
theo modulo p thƬ C(p+1)/2 ŗ 1(mod p).
VƬ thįŗæ , hai cÄn bįŗc hai cį»§a C modulo p lĆ ±C(p+1)/4mod p. TĘ°Ę”ng
tį»±, hai cÄn bįŗc hai cį»§a C modulo q lĆ ±C(p+1)/4mod q. Sau
ÄĆ³ ta cĆ³ thį» thu ÄĘ°į»£c bį»n cÄn bįŗc hai cį»§a x1 cį»§a C modulo n bįŗ±ng
cĆ”ch dĆ¹ng Äį»nh lĆ½ phįŗ§n dĘ° China.
Nhįŗn xĆ©t:
Mį»t Äiį»u lĆ½ thĆŗ lĆ vį»i p ŗ1
(mod 4), ngĘ°į»i ta chĘ°a biįŗæt ÄĘ°į»£c mį»t thuįŗt toĆ”n tįŗ„t Äį»nh theo thį»i gian Äa thį»©c
nĆ o Äį» tĆnh cÄn bįŗc hai cį»§a cĆ”c thįŗ·ng dĘ° bįŗc hai theo modulo p . Tuy nhiĆŖn, vįŗ«n
cĆ³ thuįŗt toĆ”n Las Vegas vį»i thį»i gian Äa thį»©c Äį» tĆnh nĆ³ .
Mį»t khi ÄĆ£ xĆ”c Äį»nh bį»n giĆ” trį» cĆ³ thį» cį»§a x1, ta tĆnh x
tį»« phĘ°Ę”ng trƬnh x=x1-B/2 Äį»
tƬm ÄĘ°į»£c bį»n bįŗ£n rƵ cĆ³ thį». Äiį»u nĆ y dįŗ«n Äįŗæn cĆ“ng thį»©c giįŗ£i mĆ£ sau:
![]()
VĆ dį»„ 4.13
Ta xįŗ½ minh hoįŗ” cĆ”c thį»§ tį»„c mĆ£
hoĆ” vĆ giįŗ£i mĆ£ Äį»i vį»i hį» mįŗt Rabin mį»t vĆ dį»„ nhį». Giįŗ£ sį» n=77=7“11 vĆ B=9. Khi ÄĆ³ hĆ m mĆ£ hoĆ”
lĆ
eK(y)=x2+9x
mod 77
vĆ hĆ m giįŗ£i mĆ£ lĆ
![]()
Giįŗ£ sį» Bob muį»n giįŗ£i mĆ£ bįŗ£n mĆ£ y=22. Äiį»u cįŗ§n thiįŗæt trĘ°į»c tiĆŖn lĆ tƬm cĆ”c cÄn bįŗc hai cį»§a 23 theo modulo 7 vĆ modulo 11. VƬ cįŗ£ 7 va11 Äį»u Äį»ng dĘ° vį»i 3 modulo 4 nĆŖn ta cĆ³
23(7+1)/4 ŗ 22 ŗ 4 mod 7
vĆ 23(11+1)/4ŗ 13 ŗ 1 mod 7
Sį» dį»„ng Äį»nh lĆ½ phįŗ§n dĘ° China, ta sįŗ½ tĆnh ÄĘ°į»£c bį»n cÄn bįŗc hai cį»§a
23 theo modulo 77 lĆ ±10, ±32 mod 77 . Cuį»i cĆ¹ng bį»n bįŗ£n giƵi cĆ³ thį» lĆ :
10- 43 mod 77=44
67- 43 mod 77=24
32- 43 mod 77=66
45- 43 mod 77= 2
CĆ³ thį» kiį»m tra lįŗ”i rįŗ±ng, mį»i mį»t bįŗ£n rƵ nĆ y Äį»u ÄĘ°į»£c mĆ£ hoĆ” thĆ nh mį»t bįŗ£n mĆ£ 22.
BĆ¢y giį» chĆŗng ta xįŗ½ thįŗ£o luįŗn vį» Äį»
mįŗt cį»§a hį» Rabin. Ta xįŗ½ chį»©ng minh rįŗ±ng mį»t thuįŗt toĆ”n giįŗ£i mĆ£ giįŗ£ Äį»nh A cĆ³
thį» ÄĘ°į»£c dĆ¹ng nhĘ° mį»t chĘ°Ę”ng trƬnh con trong mį»t thuįŗt toĆ”n Las Vegas Äį» phĆ¢n
tĆch modulo n vį»i xĆ”c suįŗ„t tį»i thiį»u bįŗ±ng 1/2. Thuįŗt toĆ”n nĆ y ÄĘ°į»£c mĆ“ tįŗ£ į» hƬnh
4.14.
CĆ³ mį»t sį» Äiį»m cįŗ§n ÄĘ°į»£c giįŗ£i thĆch į» ÄĆ¢y. TrĘ°į»c hįŗæt ta thįŗ„y rįŗ±ng
![]()